分野




総則
対称性
- 問題の図形の対称性を確認.
- 思考領域を限定.
座標
自分で適切な座標を設定する.
表記
ベクトルは縦書きができるが,座標は縦書きができない.
計量
計量しづらい位置に点がある場合,その点を含む直線上の点で計量しやすい位置にあるものを用いて一度計量を行なってから,分点定理や方べきの定理,ベクトルなどで比を求める.
相対性
点が領域を動くとき,点は固定されていて領域が動くと考えることもできる.
縮拡
光の投影では,1点からの縮拡が起こる.
作図
総則
優先順位
- 形状確定多角形(正多角形など)
- 形状確定曲線(円など)
- その他の多角形
- その他の曲線
立体
並行な2平面は,それぞれの枠を作り,重ならないように上下に作図する.
それぞれの平面の平面図を書くのも有効.
n角形
必要な点だけを書く.
円
対称性
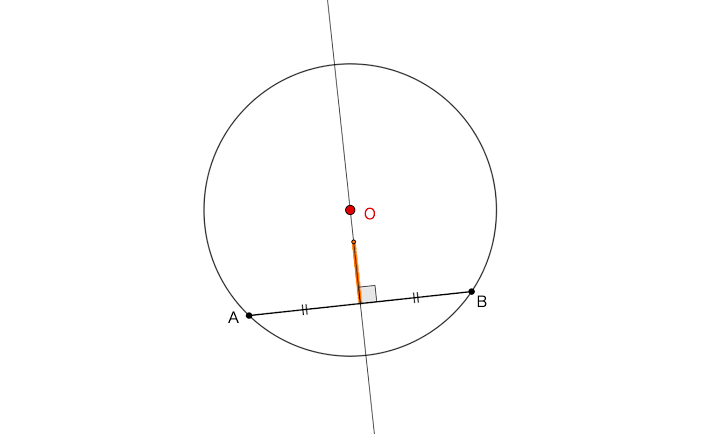
点と直線の距離
円周角の定理
直径の円周角は全て直角三角形 → 挟辺は互いに垂線.
円の内外を判断する時や相似等を示すときに使う.
正弦定理
三角形の一辺と2つ以上の角度がわかっているときに使う.
直角三角形の斜辺はその三角形の外接円の直径に等しい.
接弦定理
方冪の定理
円に関係する線分の長さを求めるとき,および同一円周上の判定(逆の成立検討)に使う.
円と共有点をもつ2直線とそれら交点からなる相似な三角形を見つける.
五心
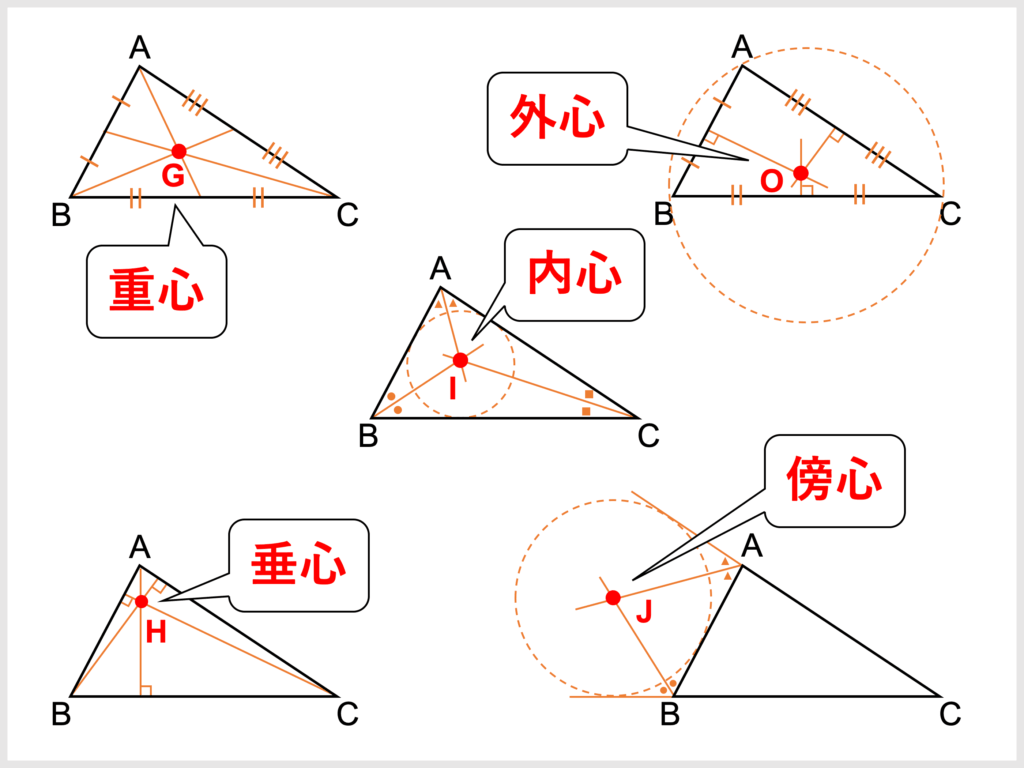
重心


位置ベクトルは,
| \[\boldsymbol{g}=\frac{\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}}{3}\] |
外心
外接円の中心で,各辺の垂直二等分線の交点.
外接円の半径 \(R\) は,
| \[R=\frac{a}{2\sin\rm A}R=\frac{b}{2\sin\rm B}R=\frac{c}{2\sin\rm C}\] |
垂心
位置ベクトルは,
| \[\] |
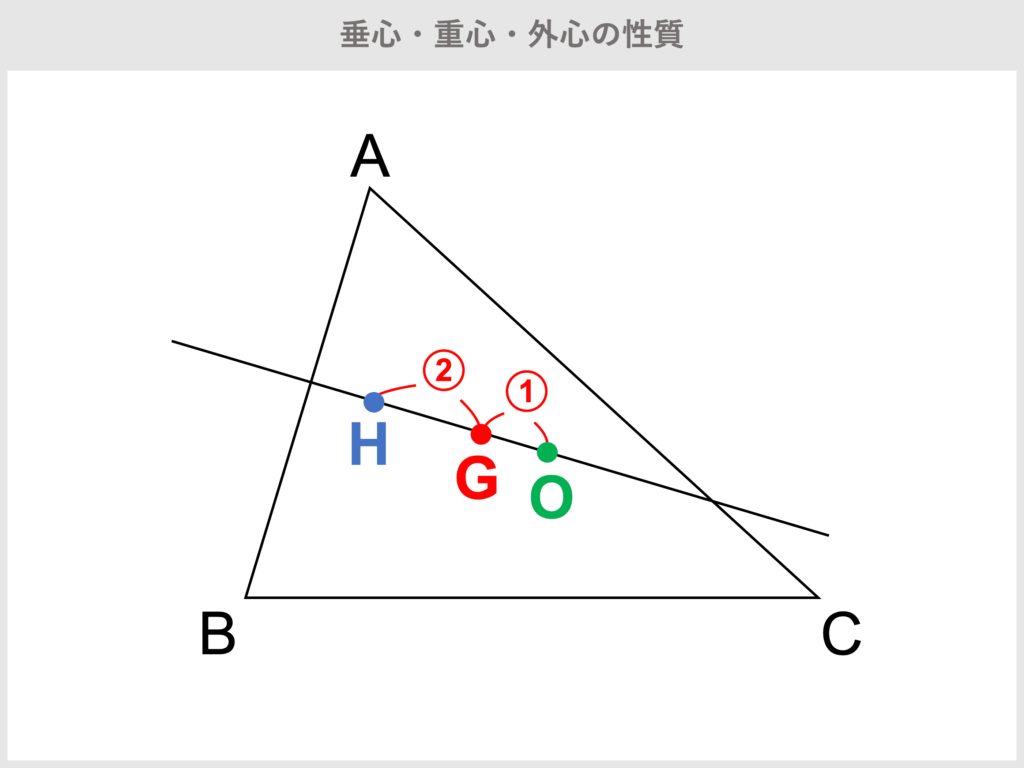
オイラー線
三角形の重心,外心,垂心はすべて同一直線上.
内心
三角形の面積を \(S\),内接円の半径を \(r\) として,
| \[S=\frac{1}{2}(a+b+c)r\] |
位置ベクトルは,
| \[\boldsymbol{i}=\frac{a\boldsymbol{a}+b\boldsymbol{b}+c\boldsymbol{c}}{a+b+c}\] |
傍心
3傍心を頂点とする三角形の垂心はもとの三角形の内心に一致する.
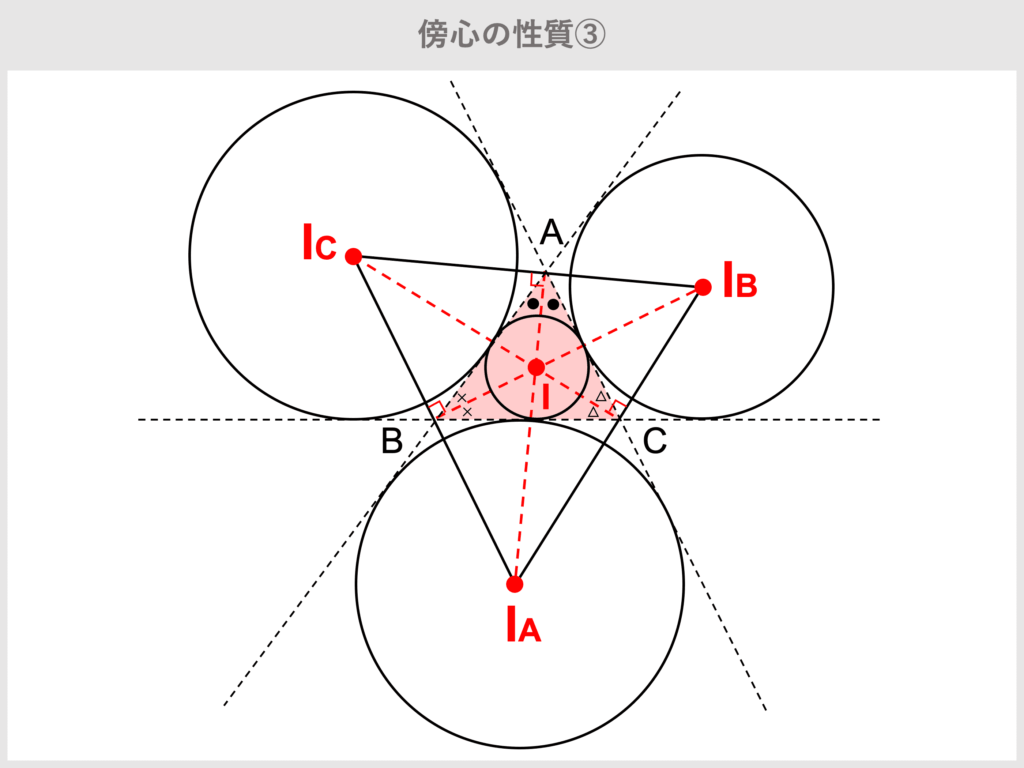
位置ベクトルは,内心のうちひとつを外分点にしたもの.
| \[\boldsymbol{i_A}=\frac{-a\boldsymbol{a}+\boldsymbol{b}b+\boldsymbol{c}c}{-a+b+c}\] |
五角形
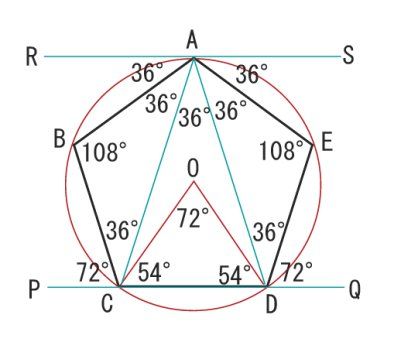
ブラーマグプタの公式
辺の長さが計算しやすい内接四角形の面積を求めるときに使う.
内接四角形の辺の長さを \(a,\,b,\,c,\,d\) として,その面積 \(S\) は,
\[s=\frac{a+b+c+d}{2},\quad S=\sqrt{(s-a)(s-b)(s-c)(s-d)}\]
\(d=0\) でヘロンの公式.
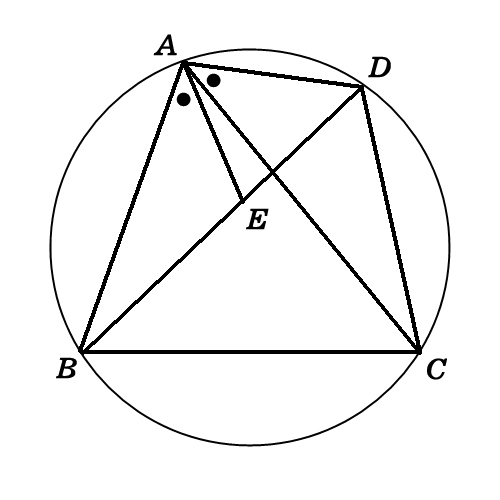
トレミーの定理
内接多角形の対角線の長さに関する問題で使う.
\[\text{四角形ABCDが円に内接}\quad\iff\quad {\rm AC}\cdot{\rm DB}
={\rm AB}\cdot{\rm DC}+{\rm AD}\cdot{\rm BC}\]
- 証明のきっかけ
\(\angle\text{CAD}=\theta\)として,\(\angle\text{BAE}=\theta\)となる補助線を引くと,\(\triangle\text{ABC}\sim\triangle\text{AED}\).
円の周上/内部/外部
円の周上の点に着目し,問われている点との位置関係を考える.
方べきの定理や円周角の定理の逆を調べるのも有効。
基礎方程式
一般複素座標を (z),一般平面座標を (x,,y),任意の実定数を (p,,q) として,
[|z-p-qi|^2=(z-p-qi)(\overline{z}-p+qi)\quad\Leftrightarrow\quad(x-p)^2+(y-q)^2]
三角関数
有名角
\(1,\,2,\,\sqrt{3}\) や \(\frac{\tau}{12},\,\frac{\tau}{6}\) を見たときは,\(1:2:\sqrt{3}\) の直角三角形を予測しておく.
一応見ておく.
| \(\cos \frac{\tau} {行\times 列}\) | \(1\) | \(3\) | \(5\) |
|---|---|---|---|
| \(2^0\) | \(1\) | \(-\frac{1}{2}\) | \(\frac{\sqrt{5}-1}{4}\) |
| \(2^1\) | \(-1\) | \(\frac{1}{2}\) | \(\frac{\sqrt{5}+1}{4}\) |
| \(2^2\) | \(0\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{10+2\sqrt{5}}}{4}\) |
| \(2^3\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{6}+\sqrt{2}}{4}\) | – |
| \(2^4\) | \(\frac{\sqrt{2+\sqrt{2}}}{2}\) | – | – |
| \(\sin \frac{\tau} {行\times 列}\) | \(1\) | \(3\) | \(5\) |
|---|---|---|---|
| \(2^0\) | \(0\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{10+2\sqrt{5}}}{4}\) |
| \(2^1\) | \(0\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{10-2\sqrt{5}}}{4}\) |
| \(2^2\) | \(1\) | \(\frac{1}{2}\) | \(\frac{\sqrt{5}-1}{4}\) |
| \(2^3\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{6}-\sqrt{2}}{4}\) | – |
| \(2^4\) | \(\frac{\sqrt{2-\sqrt{2}}}{2}\) | – | – |
| \(\tan \frac{\tau} {行\times 列}\) | \(1\) | \(3\) | \(5\) |
|---|---|---|---|
| \(2^0\) | \(0\) | \(-\sqrt{3}\) | \(\sqrt{5+2\sqrt{5}}\) |
| \(2^1\) | \(0\) | \(\sqrt{3}\) | \(\sqrt{5-2\sqrt{5}}\) |
| \(2^2\) | \(\pm \infty\) | \(\frac{1}{\sqrt{3}}\) | \(\frac{1}{\sqrt{5+2\sqrt{5}}}\) |
| \(2^3\) | \(1\) | \(2-\sqrt{3}\) | – |
| \(2^4\) | \(\sqrt{2}-1\) | – | – |
加法定理
同周期の正弦波は,どんな重なり方をしても同周期の正弦波になる.
条件の言い換え
| \[\cos\theta<0\quad\rightleftarrow\quad \frac{\tau}{4}<\theta<\frac{3}{4}\tau\mod\tau\] |
分点
総則
ある直線を比の値が異なるように \(a:b,\;c:d\) で分割するとき,その直線を \(gcd(a+b,\;c+d)\) 等分すると計算しやすい.
分点定理
\(\triangle\)ABCが存在し,直線BC,CA,AB上に点D,E,Fが存在するとき,
\[\rm直線AD,BE,CFが一点で交わる\;or\;DEFが一直線上
\quad\Leftrightarrow\quad
\rm\frac{AF}{FB}\frac{BD}{DC}\frac{CE}{EA}=1\]
1つ目がチェバの定理,2つ目がメネラウスの定理.
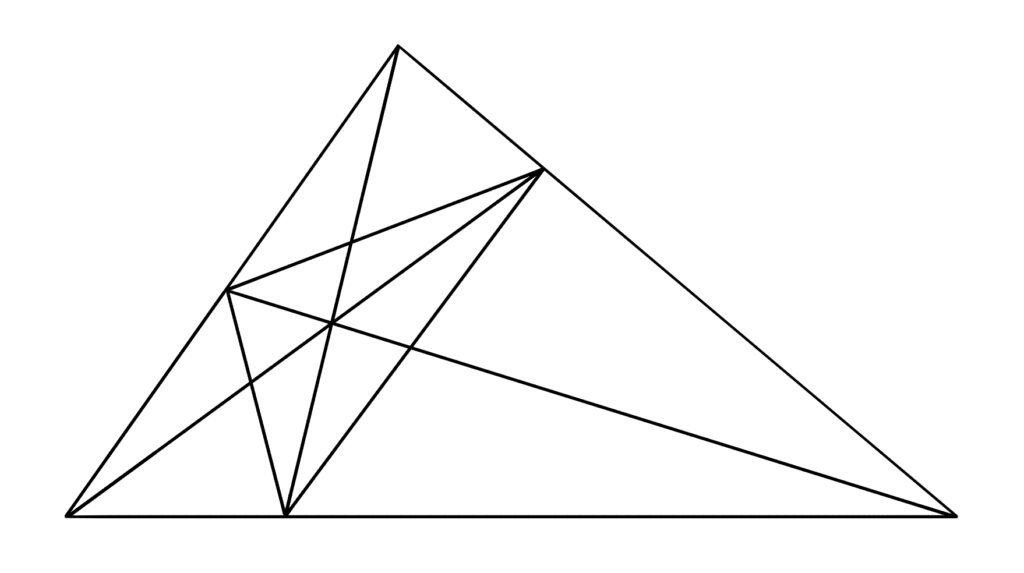
ベクトル
総則
式展開を特に丁寧に.
ある \(n\) 次元空間上の点は,その空間上の文字のみで記述される。
基本式
\[\begin{cases}\overrightarrow{\rm OB}-\overrightarrow{\rm OA}
=\overrightarrow{\rm AB}\\\\
\overrightarrow{\rm OA}+\overrightarrow{\rm AB}
=\overrightarrow{\rm AB}\end{cases}\]
大きさ
ベクトルの大きさは,各直交成分の2乗和.
内積
角度
\[\begin{align}\rm\triangle OAB\,が鋭角三角形&\quad\Leftrightarrow
\quad\begin{cases}\boldsymbol{a}\cdot\boldsymbol{b}>0\\\\
|\boldsymbol{a}|^2-\boldsymbol{a}\cdot \boldsymbol{b}>0\\\\
|\boldsymbol{b}|^2-\boldsymbol{a}\cdot\boldsymbol{b}>0
\end{cases}\quad(\rm and)\\\\
\rm\triangle OAB\,が直角三角形&\quad\Leftrightarrow\quad
\begin{cases}\boldsymbol{a}\cdot\boldsymbol{b}=0\\\\
|\boldsymbol{a}|^2-\boldsymbol{a}\cdot \boldsymbol{b}=0\\\\
|\boldsymbol{b}|^2-\boldsymbol{a}\cdot\boldsymbol{b}=0
\end{cases}\quad(\rm or)\\\\
\rm\triangle OAB\,が鈍角三角形&\quad\Leftrightarrow\quad\begin{cases}
\boldsymbol{a}\cdot\boldsymbol{b}<0\\\\
|\boldsymbol{a}|^2-\boldsymbol{a}\cdot \boldsymbol{b}<0\\\\
|\boldsymbol{b}|^2-\boldsymbol{a}\cdot\boldsymbol{b}<0\end{cases}
\quad(\rm or)\end{align}\]
外積
3次元空間上で法線ベクトルを求めるときに使う.
大きさは,2ベクトルを辺にもつ平行四辺形の面積に同じ.
\[\boldsymbol{a}\times\boldsymbol{b}=\begin{pmatrix}
a_y b_z – a_z b_y\\a_z b_x – a_x b_z\\a_x b_y – a_y b_x\end{pmatrix}\]
ベクトル\(\boldsymbol{a},\,\boldsymbol{b}\)を2辺とする三角形の面積\(S\)は,
\[S=\frac{1}{2}|\boldsymbol{a}\times\boldsymbol{b}|=\frac{1}{2}
\sqrt{|\boldsymbol{a}|^2|\boldsymbol{b}|^2
-(\boldsymbol{a}\cdot\boldsymbol{b})^2}\]
特に,\(z\)成分がないとき,
\[S=\frac{1}{2}|a_x b_y – a_y b_x|\]
複素数
偏角は範囲を常に確認する.
| \[z = \bar{z} \iff z \in \mathbb{R}\] |
基礎方程式
一般複素座標を \(z\),一般平面座標を \(x,\,y\),任意の実定数を \(p,\,q\) として,
| \[|z-p-qi|^2=(z-p-qi)(\overline{z}-p+qi)\quad\Leftrightarrow\quad(x-p)^2+(y-q)^2\] |
二次曲線と極座標
接線
接線を \(y=ax+b\) とすると,
二次曲線 \(f(x,\,y)=0\) に対し,方程式 \(f(x,\,ax+b)\) の判別式 \(D\) が \(0\) となるように \(a,\,b\) を定める.
n乗根
1つ解を見つけて複素単位円をn等分.
\[z=e^{i\theta},\,z^{\frac{1}{n}}=e^{i\frac{\theta+\tau k}{n}}(n,k\in\mathbb{N})\]
\(x=\cos\frac{k}{n}\tau\)
\[\begin{align}&\omega^{n}=1\quad(\omega\ne1,\,n=2m+1)\\\\
\Leftrightarrow\quad
&\sum_{k=1}^m (\omega^k+\omega^{(2m+1)-k})+1=0\\\\
\Leftrightarrow\quad&2\sum_{k=1}^m \cos\frac{k}{2m+1}\tau+1=0\\\\
\rightarrow\quad&\begin{cases}4x^2+2x-1=0\quad(n=5)\\\\
8x^3+4x^2-4x-1=0\quad(n=7)\end{cases}\end{align}\]
最後は倍角の公式でばらす.
\(n\) が偶数の場合,半角の公式から \(x=2x’\,^2-1\) を代入する.
離心率
二次曲線Cに対し,準線との距離をCP,焦点をFとして,離心率eは,
\[\frac{\rm CF}{\rm CP}={e}\]
二次曲線の一般形
原点を焦点とし,点\((0,\,\pm d)\)を通る二次曲線は,
\[\Biggl(\frac{\frac{x}{d}+\frac{e}{1-e^2}}{\frac{1}{1-e^2}}\Biggr)^2
+\Biggl(\frac{\frac{y}{d}}{\frac{1}{\sqrt{1-e^2}}}\Biggr)^2=1
\quad\iff\quad r=\frac{d}{1+e\cos{\theta}}\\\]
原点を焦点とし,\(x=p\)を準線とする二次曲線は,
\[\Biggl(\frac{\frac{x}{p}+\frac{e^2}{1-e^2}}{\frac{e}{1-e^2}}\Biggr)^2
+\Biggl(\frac{\frac{y}{p}}{\frac{e}{\sqrt{1-e^2}}}\Biggr)^2=1
\quad\iff\quad r=\frac{ep}{1+e\cos{\theta}}\]
円
焦点からの距離が等しい点の集合.
\[x^2+y^2=r^2\quad(e=0)\]
性質
楕円
2焦点との距離の和が等しい点の集合.
\[\Biggl(\frac{x+\sqrt{a^2-b^2}}{a}\Biggr)^2
+\biggl(\frac{y}{b}\biggr)^2=1\quad(0<e<1)\]
性質
半径\(\sqrt{a^2+b^2}\) の準円をもつ.
面積
上の楕円の面積は,\(\pi ab\) .
楕円の面積を部分的に求めるときは,座標変換を行ってできる円の面積から求められないか考える.
放物線
焦点との距離と準線との距離が等しい点の集合.
\[y^2=4p(x+p)\quad(e\rightarrow 1)\]
性質
半径\(\infty\) の準円(=準線)をもつ.
双曲線
2焦点との距離の差が等しい点の集合.
ちなみに,\(e\rightarrow\infty\)の極限は1本の準線に収束する.
\[\Biggl(\frac{x-\sqrt{a^2+b^2}}{a}\Biggr)^2
-\biggl(\frac{y}{b}\biggr)^2=1\quad(e>1)\]
性質
半径\(\sqrt{|a^2-b^2|}\) の準円をもつ.
束
2つ以上のグラフが2つ以上の交点をもつ場合に使う.
\[\sum_i a_i f_i(\boldsymbol{x_0})=0\quad(a_i\in\mathbb{R})
\quad\Longleftrightarrow\quad\sum_i a_i f_i(\boldsymbol{x})=0
\text{ は点 \(\boldsymbol{x_0}\) を通る.}\]
極線
二次曲線の極線を求める際の変換則は,
\[\begin{align}x^2&\quad\longrightarrow\quad xx_0\\\\
y^2&\quad\longrightarrow\quad yy_0\\\\
xy&\quad\longrightarrow\quad\frac{xy_0+x_0 y}{2}\\\\
x&\quad\longrightarrow\quad\frac{x+x_0}{2}\\\\
y&\quad\longrightarrow\quad\frac{y+y_0}{2}\end{align}\]