分野




計算
式量
元素
| 元素 | 式量 [g/mol] |
|---|---|
| \(\rm H\) | \(1\) |
| \(\rm C\) | \(12\) |
| \(\rm N\) | \(14\) |
| \(\rm O\) | \(16\) |
| \(\rm Na\) | \(23\) |
| \(\rm Mg\) | \(24.3^*\) |
| \(\rm Al\) | \(27\) |
| \(\rm S\) | \(32\) |
| \(\rm Cl\) | \(35.5^*\) |
| \(\rm K\) | \(39\) |
| \(\rm Ca\) | \(40\) |
| \(\rm Fe\) | \(56\) |
| \(\rm Zn\) | \(65\) |
| \(\rm Ag\) | \(108\) |
| \(\rm I\) | \(127\) |
| \(\rm Ba\) | \(137\) |
化合物
| 化学式 | 式量 [g/mol] |
|---|---|
| \(\rm C_6H_{12}O_6\) | \(180\) |
| \(\rm C_{12}H_{22}O_{11}\) | \(342\) |
| \(\rm(C_6H_{10}O_5)_{\it n}\) | \(162n\) |
| \(\rm CO_2\) | \(44\) |
| \(\rm HCl\) | \(36.5^*\) |
| \(\rm HNO_3\) | \(63\) |
| \(\rm H_2O\) | \(18\) |
| \(\rm H_2SO_4\) | \(98\) |
| \(\rm NaCl\) | \(58.5^*\) |
| \(\rm NaOH\) | \(40\) |
計算テクニック
| 計算テクニック | 有効桁数 |
|---|---|
| \[22.4=2^5\cdot7\times10^{-1}\approx\frac{20}{9}\] | 2 |
| \[8.31\approx\frac{25}{3}\] | 2 |
分子・結晶
溶液
溶解表
| [\(\rm{}^{\circ}C\)]\[g] | \[\rm H_2O\] | \[\rm S\] |
|---|---|---|
| \[T_0\] | ||
| \[T_1\] |
pH
公式
物質 \(X\) の濃度を \(\bigl[X\bigr]\;\rm[mol/L]\),モル濃度を \(C\;\rm[mol/L]\),体積を \(V\;\rm[L]\),電離度を \(\alpha\;[\text{-}]\),酸・塩基を \(\rm a,\;b\) として,
\[\begin{align}
&\bigl[{\rm H^+}\bigr]=C_{\rm a}V\alpha\\\\
&\bigl[{\rm OH^-}\bigr]=C_{\rm b}V\alpha
\end{align}\]
また,水のイオン積を \(K_{\rm w}\;\rm[mol^2/L^2]\) として,
\[
K_{\rm w}=\bigl[H^+\bigr]\bigl[OH^-\bigr]\approx1.0\times10^{-14}
\]
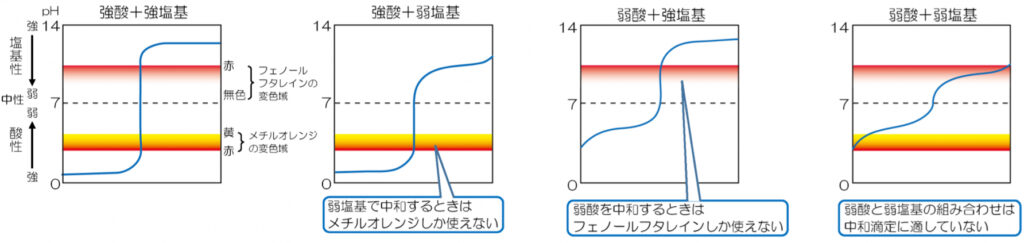
指示薬
上下が入れ替わった場合も然り.
変色域は,
- フェノールフタレイン:\(\rm pH\;8.0\sim9.8\)
- メチルオレンジ:\(\rm pH\;3.1\sim4.4\)
BTB溶液は連続的な変色をするので,中和滴定の指示薬には向いていない.
中和滴定
公式
モル濃度を \(C\;\rm[mol/L]\),体積を \(V\;\rm[L]\),価数を \(k\;\rm[\text{-}]\),酸・塩基を \(\rm a,\;b\) として,
\[
\sum_{\rm a} C_{\rm a} V_{\rm a} k_{\rm a}
=\sum_{\rm b} C_{\rm b} V_{\rm b} k_{\rm b}
\]
または,体積を \(v\;\rm[mL]\) として,
\[
\sum_{\rm a} C_{\rm a} v_{\rm a} k_{\rm a}
=\sum_{\rm b} C_{\rm b} v_{\rm b} k_{\rm b}
\]
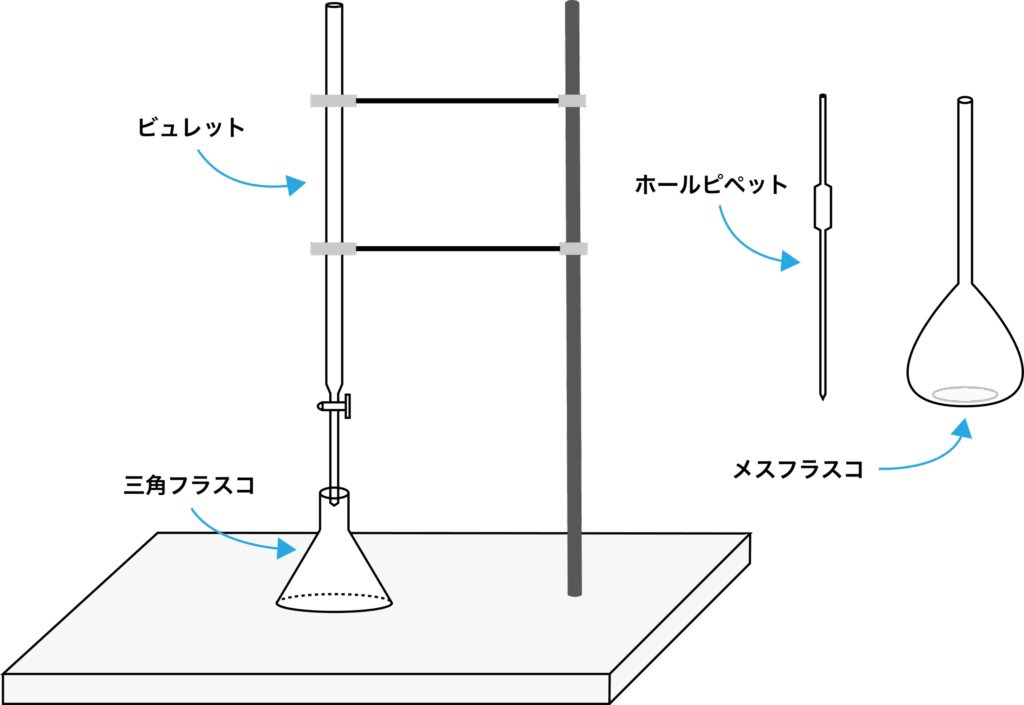
操作
- 標準溶液を「メスフラスコ」で調製する.
- 標準溶液を「ホールピペット」で量り取る.
- 標準溶液を「三角フラスコ」に移す.
- 濃度不明の溶液を「ビュレット」で滴下する.
- 不都合な濃度変化をさせないため,
- ホールピペットとビュレットは共洗いを行う.
- コニカルビーカーは共洗いを行わない.
- 三角フラスコの代わりに「コニカルビーカー」を用いる場合もある.
- ホールピペットは口で吸い上げる場合がある.
- 安全面から「安全ピペッター」を用いる場合がある.
半透膜
ファントホッフの法則
何がどちらへ移動するか図に書く.
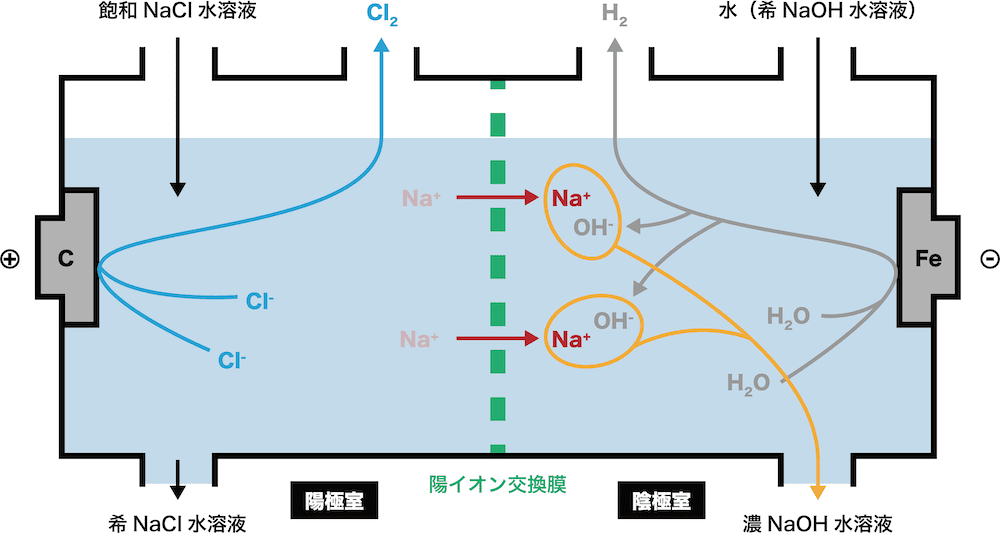
イオン交換膜法
水酸化ナトリウムを濃くし,塩素と水素の単体を取り出す.
ラウールの法則
純溶媒の蒸気圧を \(P_l’\),その溶媒のモル分率を \(x_l\) として,蒸気圧 \(P_l\) は,
| \[P_l’=P_lx_l\] |
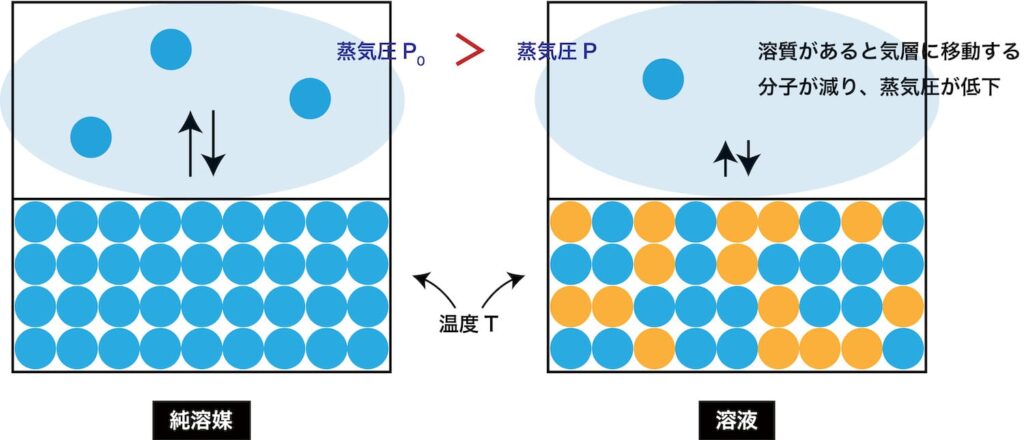
蒸気圧降下
純溶媒時の蒸気圧を \(P_l\),その溶媒の物質量を \(n_l\),電離・会合等を考慮した式量を \(M_n\),溶質の物質量を \(n_s\) として,実際の溶媒の蒸気圧 \(P_l’\) は,
| \[{\it \Delta}P=\frac{n_s}{n_l\color{#bbb}{+n_s}}P_l \approx\underset{モル凝固点降下度\,K}{\underline{P_lM_l\times10^{-3}}}\times \underset{実質質量モル濃度 m}{\underline{\frac{n_s}{n_lM_l\times10^{-3}}}} =Km\] |
気体
基礎方程式
上から,気体の状態方程式,ファントホッフの法則,ヘンリーの法則,ドルトンの法則.
\[\begin{align}
&pV=nRT\\
&{\it\Pi}=CRT=\frac{\rho}{M}RT&&({\it\Pi}V=nRT)\\
&\frac{p}{n}=Const.\\
&\frac{n_1}{n_0}=\frac{p_1}{p_0}&&(p=p_0+p_1)
\end{align}\]
関係する液体がすべて気化した場合,気体の存在比の公式が使える.
気体計算では,バランスシートを書く.
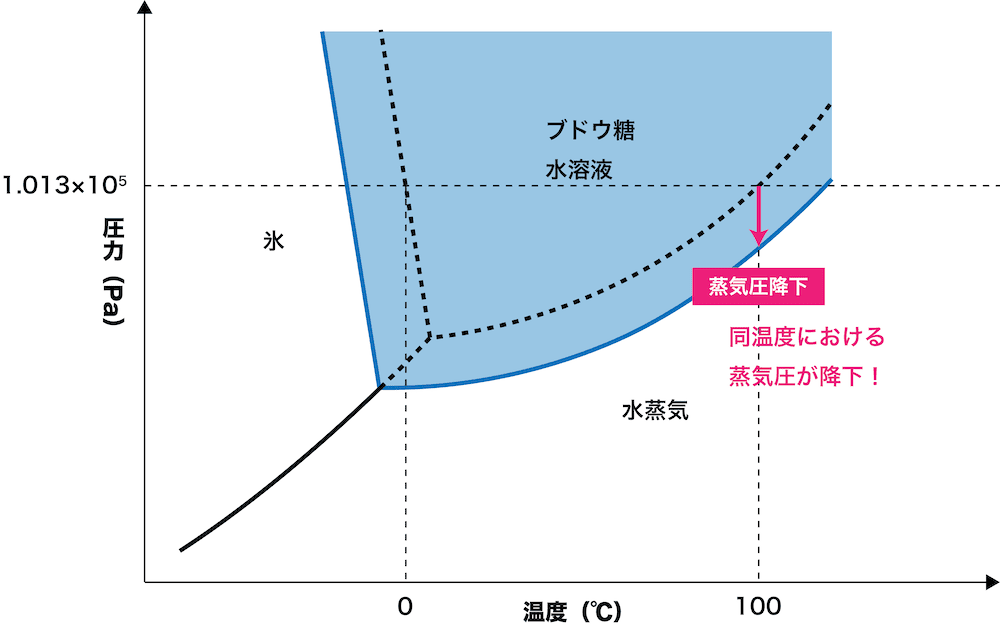
状態図
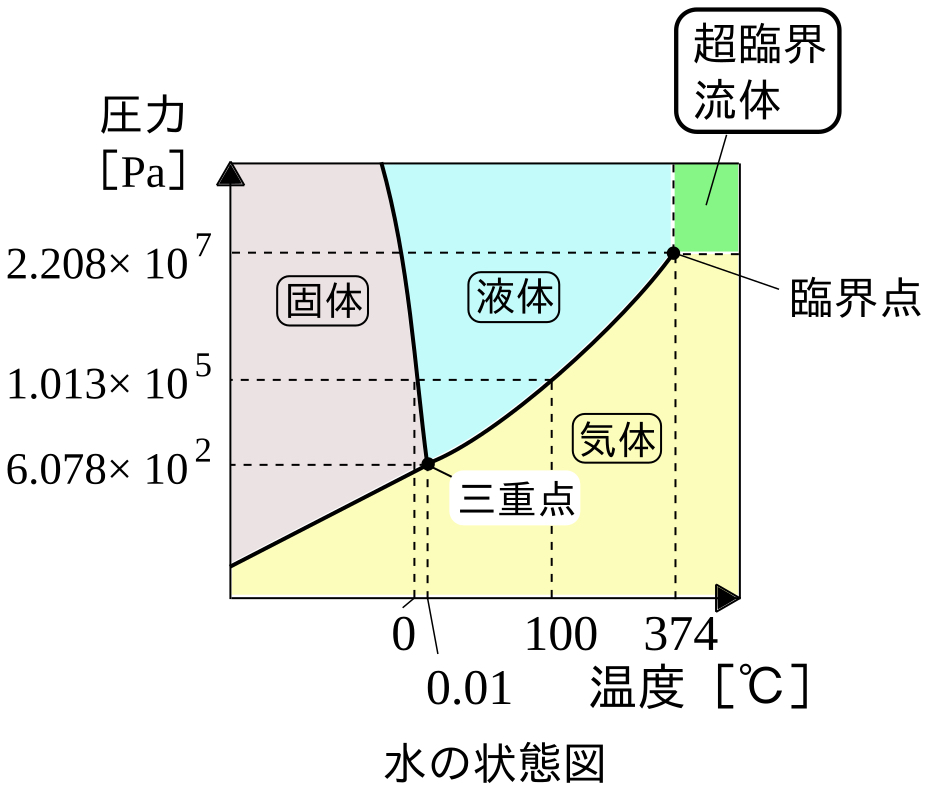
圧力と状態変化
圧力と沸点・昇華点は単調増加,圧力と融点は単調減少の関係にある.
蒸気圧
液体発生の場合,分圧と蒸気圧は等しい.
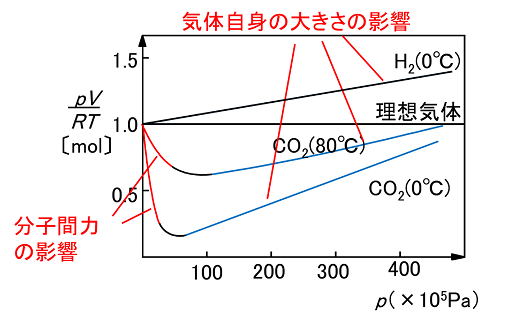
圧縮率因子
低圧ならば分子間力が,高圧ならば体積の影響が大きくなる.
| \[Z=\frac{PV}{nRT}\approx1\] |
酸化還元反応
電池
1 つの電子が \(n\)個分の活物質を通るので,電池を \(n\) 個直列接続すると,単位電子あたりに消費される活物質は \(n\) 倍
エンタルピー・エントロピー
主要エンタルピー
| 種類 | 補足 |
|---|---|
| 中和エンタルピー | \({\it\Delta}H=-55.8\) |
熱の発生
\(n\;\rm[mol]\) ある物質の \(1\;\rm[mol]\) の反応エンタルピーを \({\it \Delta} H\;\rm[kJ/mol]\),反応後の周辺の物体の比熱を \(c\;\rm[J/(g\cdot K)]\),質量を \(m\;\rm[g]\) ,温度変化を \(T\;\rm[K]\)として,
\[
n{\it \Delta}H=-cm{\it \Delta}T\times\frac{1}{1000}
\]
平衡
温度一定 \(\Rightarrow\) 平衡定数一定.
これを実現するためにルシャトリエの原理がある.
反応速度
濃度 \(C\),温度,触媒,表面積に依存.
触媒は活性化エネルギーを小さくするが,エンタルピーは変化させない.
反応速度定数 \(k\) は主反応に左右されるため,実験算出.
| \[v=k\frac{dC}{dt}\;(>0)\] |
主な触媒
- 不均一触媒:反応物と状態が異なるもの
| 触媒 | 用例 |
|---|---|
| 酸化マンガン(Ⅳ) | 過酸化水素水の分解 |