総則
総則
落ち着いて問題を解く.
誘導の指示に従う.
作用する物理量の主語をよく確認する.
最後に単位を確認する.
限界を問われたら,不等式を立てて計算する.
合図
| 合図 | タイミング |
|---|---|
| \(\bigcirc\) | 使用可能量(文章,図),静止 |
| \(\boldsymbol{\bigcirc}\) | 求量 |
| \(\_\_\!/\) | 重要 |
| 以下では\(\tau=2\pi\) を用いる | 円運動や単振動の解答用紙の上部に |
| OK | 解答後,使用可能量のみで解答していれば問題用紙に |
| \(\bullet\;\circ\) | 腹 節 |
グラフ・大小関係
- グラフ間の差異などから,問われている物理量を調べる.
特に,グラフは端点や特異点,重なり方に注目. - 問われている物理量と相関のある適切な物理量を選ぶ.
- 状態を横,物理量を縦に並べた増減表を描く.
状態間には,起きたことを書く. - 不明な大小を調べ,小さい方から大きい方へ矢印を引く.
- 結果を小さい順に並べ,問に即して回答する.
力学
座標
座標設定
最初に適切な座標設定を行う.
座標変換
座標変換をするときは,変換則を書く.
問題文に特別な指示がない限り,電磁気の問題で座標変換はしないほうが良い.
時刻 \(t\) での対象物の位置を \((x,\,y)\),観測者の変位を \((X,\,Y)\) として,
| \[\begin{pmatrix}x\\y\end{pmatrix} \longrightarrow\begin{pmatrix}x’\\y’\end{pmatrix} =\begin{pmatrix}x-X\\y-Y\end{pmatrix}\\ \begin{pmatrix}\dot{x}\\\dot{y}\end{pmatrix} \longrightarrow\begin{pmatrix}\dot{x}’\\\dot{y}’\end{pmatrix} =\begin{pmatrix}\dot{x}-\dot{X}\\\dot{y}-\dot{Y}\end{pmatrix}\\ \begin{pmatrix}\ddot{x}\\\ddot{y}\end{pmatrix} \longrightarrow\begin{pmatrix}\ddot{x}’\\\ddot{y}’\end{pmatrix} =\begin{pmatrix}\ddot{x}-\ddot{X}\\\ddot{y}-\ddot{Y}\end{pmatrix}\] |
運動方程式
実際の加速度を\(\boldsymbol{a}\),物体にかかる合力を\(\boldsymbol{F}\)として,原則,2方向で立てる.
右辺を0とするのは,該当する\(\boldsymbol{a}\)の成分が0だと判断できた後.
\(x\text{-}y\) 運動方程式
床や斜面に対して使う.
斜面の場合,対応する角度に注意.
また,重力の斜面垂直成分を実質重力とみなせる.
摩擦力は同速度物体間に働かない.
| \[\begin{align}&並行成分を\,x,\;垂直成分を\,y\,として,&& &&\\\\ &\begin{pmatrix}F_x\\F_y\end{pmatrix} =m\begin{pmatrix}a_x\\a_y\end{pmatrix}\end{align}\] |
\(r\text{-}\theta\) 運動方程式
等速円運動で,主に半径\(r\),角速度\(\omega\),速度\(v\,(=r\omega)\)を導くために使う.
その後,円の性質に注目し,使える角度がないか調べる.
| \[\begin{align}&向心力を\,F_r,\;接線方向の合力を\,F_\theta\,として,&& &&\\\\ &\begin{pmatrix}mr\omega^2-F_r\\F_\theta\end{pmatrix} =\begin{pmatrix}0\\0\end{pmatrix}\end{align}\] |
一定磁場下で自由電荷が等速円運動する場合,向心力はローレンツ力のみ.
主な力
| 力 | 一般形 |
|---|---|
| 重力(小規模) | \[m\boldsymbol{g}\] |
| 垂直抗力 | \[\boldsymbol{N}\] |
| ばねの弾性力 | \[-k(\boldsymbol{x}-l_0)\] |
| 張力 | \[\boldsymbol{T}\] |
| 摩擦力 | \[m\boldsymbol{g}\mu\] |
| 浮力 | \[\rho V\boldsymbol{g}\] |
| 流体抵抗 | \[-k\boldsymbol{v}\] |
| 遠心力 | \[m\boldsymbol{r}\omega^2 =m\frac{v^2}{r} \frac{\boldsymbol{r}}{r}\] |
| クーロン力・ローレンツ力(荷電粒子) | \[q(\boldsymbol{E} +\boldsymbol{v}\times\boldsymbol{B})\] |
| ローレンツ力(電流) | \[\boldsymbol{I}\times\boldsymbol{B}l\quad \biggl(=-\frac{\boldsymbol{v}B^2l^2} {R}\biggr)\] |
| 重力(宇宙規模) | \[G\frac{Mm}{r^2}\frac{\boldsymbol{r}}{r}\] |
孤立系
定義
| \[\begin{align}&物体\,i\,が物体\,j\,に及ぼす内力を\,F_{ij}\,として,&&\\\\ &m_i\ddot{x}_i=\sum_{j}F_{ji}\;,\quad\sum_i m_i\ddot{x}_i=0\end{align}\] |
重心と運動量保存則
| \[\begin{align} &&&\sum_i m_i\ddot{x}_G=\sum_i m_i\ddot{x}_i=0&&(重心化運動方程式)&&&\\\\ &\Leftrightarrow& &\sum_i m_i\dot{x}_G=\sum_i m_i\dot{x}_i=Const.&&(運動量保存則)\\\\ &\Leftrightarrow& &x_G=\frac{\sum_i m_ix_i}{\sum_i m_i}=x_G|_{t=0}+x_G t&&(重心の慣性運動) \end{align}\] |
運動量保存則は,静止した場合にもよく使う.
このとき,2体問題の場合は特にエネルギー比との組み合わせが頻出.
| \[\begin{align}&M\boldsymbol{V}+m\boldsymbol{v}=0&&\Rightarrow&& \cfrac{\dfrac{1}{2}MV^2}{\dfrac{1}{2}mv^2}=\frac{V}{v}=\frac{m}{M}\end{align}\] |
2体問題
1. 運動方程式
| \[\begin{align}&\begin{cases}m_1\ddot{x}_1=-F_{12}\\\\ m_2\ddot{x}_2=F_{12}\end{cases}\end{align}\] |
2. 相対エネルギー保存則
| \[\begin{align}&\begin{aligned}&&&\ddot{x}_{12}=\ddot{x}_2-\ddot{x}_1\\\\ &\Leftrightarrow&&\frac{m_1m_2}{m_1+m_2}\ddot{x}_{12} =\frac{m_1}{m_1+m_2}F_{12}-\frac{m_2}{m_1+m_2}(-F_{12})\\\\ &\Leftrightarrow&&\mu\ddot{x}_{12}=F_{12} \qquad\underset{換算質量}{\underline{\Biggl(\mu=\frac{m_1m_2}{m_1+m_2} =\frac{1}{\frac{1}{m_1}+\frac{1}{m_2}}\Biggr)}}\\\\ &\Leftrightarrow&&\dot{x}_{12}\frac{d}{dt}(\mu\dot{x}_{12}) =F_{12}\frac{dx_{12}}{dt}\\\\ &\Leftrightarrow& &\frac{d}{dt}\biggl(\frac{1}{2}\mu\dot{x}_{12}^2\biggr)=-\frac{dU_{12}}{dt}\\\\ &\Rightarrow&&K_{12}+U_{12}=Const.\\\\\end{aligned}\end{align}\] |
3. 運動エネルギーの恒等式
| \[\begin{align}&\frac{1}{2}m_1\dot{x}_{1}^2+\frac{1}{2}m_2\dot{x}_{2}^2\\\\ =\quad&\frac{1}{2}m_1(\dot{x}_{G}+\dot{x}_{G1})^2 +\frac{1}{2}m_2(\dot{x}_{G}+\dot{x}_{G2})^2\\\\ =\quad&\frac{1}{2}(m_1+m_2)\dot{x}_G^2 +\frac{1}{2}m_1\dot{x}_{G1}^2+\frac{1}{2}m_2\dot{x}_{G2}^2 +\underset{0}{\underline{(m_1\dot{x}_{G1}+m_2\dot{x}_{G2})}}\dot{x}_G\\\\ =\quad&\frac{1}{2}(m_1+m_2)\dot{x}_G^2 +\frac{1}{2}m_1\dot{x}_{G1}^2+\frac{1}{2}m_2\dot{x}_{G2}^2 -\underset{0}{\underline{\frac{1}{2} \frac{(m_1\dot{x}_{G1}+m_2\dot{x}_{G2})^2}{m_1+m_2}}}\\\\ =\quad&\underset{重心系で\,0}{\underline{\frac{1}{2}(m_1+m_2)\dot{x}_G^2}} +\frac{1}{2}\mu\dot{x}_{12}^2\end{align}\] |
力積(非孤立形)
\(t=t_0\) から \(t=t_1\) まで力 \(f(t)\) が働いたとき,力積 \(I\) は,
| \[\boldsymbol{I}=\int_{t_0}^{t_1}\boldsymbol{F}(t)\,dt=m{\it\Delta\boldsymbol{\dot{x}}}\] |
保存系
保存力
電磁気力・重力の2種類のみ.(弾性力 \(\in\) 電磁気力)
保存力の仕事は,運動の様子に関わらず,力学的エネルギー変化に等しい.
| \[{\it\Delta}U=-W_{\rm out}=-\boldsymbol{F}\cdot{\it\Delta}\boldsymbol{x}\] |
エネルギー保存則
保存系の物体の変化の総量を求めるために使う.
| \[\begin{align} &E=\underset{U}{\underline{qV+\frac{1}{2}kx^2+mgh}} +\underset{K}{\underline{\frac{1}{2}m\ddot{x}^2}}=Const.&&(小規模)\\\\ &E=-G\frac{Mm}{r}+\frac{1}{2}m\ddot{x}^2=Const.&&(大規模)&&\end{align}\] |
反発係数(C.O.R.)
エネルギー保存則に位置エネルギーが登場しない場合,弾性運動とみなして計算できる.
| \[\begin{align}&e=-\frac{\dot{x}_2’-\dot{x}_1’}{\dot{x}_2-\dot{x}_1}\\\\ &e=1\quad\Leftrightarrow\quad \frac{1}{2}\mu \dot{x}_{12}^2=Const.\end{align}\] |
単振動
一般式
振動中心を \(x_{\rm O}\),角振動数を \(\omega\),初期位相を \(x|_{t=t_0}\),初速度を \(\dot{x}|_{t=t_0}\) として,
| \[x-x_{\rm O}=(x|_{t=t_0}-x_{\rm O})\cos{\bigl(\omega(t-t_0)\bigr)} +\frac{\dot{x}|_{t=t_0}}{\omega}\sin{\bigl(\omega(t-t_0)\bigr)}\] |
詳細
適切な座標を設定すると,以下が置ける.
\(\ddot{x}\)が\(\dot{x}\)に依存する場合,\(\ddot{x}\)の位相と初期条件も書く.
| \[\begin{cases} x-x_{\rm O}=A_0\cos{\omega t}+A_1\sin{\omega t}&&x|_{t=0}-x_{\rm O}=A_0\\ \dot{x}=-A_0\omega\sin{\omega t}+A_1\omega\cos{\omega t}&& \dot{x}|_{t=0}=A_1\omega\\ \ddot{x}=-\omega^2(x-x_{\rm O})\end{cases}\] |
まず,\(m\ddot{x}\) から振動中心 \(x_{\rm O}\) を求め,初期条件をもとに振幅\(\sqrt{A^2+B^2}\) を決定する.
振動中心 \(x_{\rm O}\) では、物体に加速度が生じない,つまり物体に働く合力が0.
| \[\ddot{x}|_{x=x_{\rm O}}=0\] |
また,時間によらず,位置と速度の関係は以下が成り立つ.
| \[|\dot{x}|=\omega\sqrt{A^2-(x-x_{\rm O})^2}\] |
ケプラーの第3法則
| \[\frac{r^3}{T^2}=Const.\] |
マクスウェル方程式
| \[\begin{align}&\boldsymbol{\nabla}\cdot \boldsymbol{E}=\frac{Q}{\varepsilon_0}\\ &\boldsymbol{\nabla}\times \boldsymbol{E} =-\frac{\partial \boldsymbol{B}}{\partial t}\\\\ &\boldsymbol{\nabla}\cdot \boldsymbol{B}=0\\\\ &\boldsymbol{\nabla}\times \boldsymbol{B} =\mu_0\epsilon_0\frac{\partial \boldsymbol{E}}{\partial t} +\mu_0\boldsymbol{B}\\\end{align}\] |
電気回路
キルヒホッフの法則
閉回路について,追加で式が欲しいときに使う.
未知の電圧や電流を一度すべて文字で置き,できるだけ多くの関係式を作る.
向きに注意.
第一法則
| \[\begin{align}&任意の閉回路内の点に流入・流出する電流\,I_i\,に対し,&& && &&\\\\ &\sum_i I_i=0\end{align}\] |
第二法則
| \[\begin{align}&任意の閉回路内で上昇・降下する電圧\,V_i\,に対し,&& && &&\\\\ &\sum_i V_i=0\end{align}\] |
コンデンサー
キャリア移動時の電位変化は,電荷が移動した
| \[\begin{align}&Q=CV\\\\ &U=\frac{1}{2}QV=\frac{1}{2}CV^2=\frac{Q^2}{2C}\end{align}\] |
電荷保存則
| \[\begin{align}&孤立部で,\\\\&Q=Const.\end{align}\] |
合成
| \[\begin{align}&コンデンサー間が孤立部かつ無帯電のとき,&& && &&\\\\ &\frac{1}{R}=\sum_i \frac{1}{R_i}\end{align}\] |
コイル
| \[\begin{align} &誘導起電力を\,V,\;\,N\,回巻きコイル内の磁束を\,{\it\Phi},\,リアクタンスを\,L,\\ &電流を\,I,\;エネルギーを\,U\,として,&& && && &&\\\\ &V=-N\frac{d\it\Phi}{dt}=-L\frac{dI}{dt}\\\\&U=\frac{1}{2}LI^2\end{align}\] |
回路のエネルギー
コンデンサーに外力を加えたり,ジュールが発生したりしたときに使う.
| \[\begin{align}&回路のエネルギー変化を\,{\it\Delta}U,\;ジュール熱を\,Q_{\rm out},\; 与えた仕事を\,W_{\rm in}\,として,&& && && &&\\\\ &U=\frac{1}{2}QV+\frac{1}{2}LI^2\\\\ &Q_{\rm out}=-{\it\Delta}U+W_{\rm in}=IVt\end{align}\] |
\(RLC\)交流回路
電圧と電流
| \[\begin{align}&起電力を\,V,\;電流を\,I\,として,\\\\ &\begin{aligned}V=RI&\quad\Rightarrow\quad I=\frac{V_0}{R}\sin\omega t\\\\ V=L\frac{dI}{dt}&\quad\Rightarrow\quad I=\frac{V_0}{L}\int \sin\omega t\;dt =\frac{V_0}{\omega L}\sin(\omega t-\frac{\tau}{4})\\\\ Q=CV&\quad\Rightarrow\quad I=CV_0\frac{d}{dt}\sin\omega t =\omega CV_0\sin(\omega t+\frac{\tau}{4})\end{aligned}\end{align}\] |
抵抗
直流接続の場合,電流を基準に合成して,
| \[I=\frac{V_0}{\sqrt{R^2+\Bigl(L\omega-\frac{1}{\omega C}\Bigr)^2}} \sin(\omega t-\phi) \qquad\Biggl(\tan\phi=\frac{L\omega-\frac{1}{\omega C}}{R}\Biggr)\] |
並列接続の場合,電圧を基準に合成して,
| \[I=V_0\sqrt{\frac{1}{R^2}+\biggl(\frac{1}{L\omega}-\omega C\biggr)^2} \sin(\omega t-\phi) \qquad\Biggl(\tan\phi=\frac{\frac{1}{L\omega}-\omega C}{\frac{1}{R}}\Biggr)\] |
今日振角周波数
共振角周波数は,
| \[\omega_0=\frac{1}{\sqrt{LC}}\] |
熱力学
重要方程式
| \[\begin{align}&上から,\;状態方程式,\;内部エネルギー,\;仕事,\;熱力学第一法則,\;比熱比.&&\\ &ただし,\;()内は単原子分子の場合.&& &&\\\\ &PV=nRT\\\\&U=nC_V T\,\biggl(=\frac{3}{2}nRT=\frac{3}{2}PV\biggr)\\\\ &W_{\rm out}=P{\it\Delta}V\,=nR{\it\Delta}T\\\\ &Q_{\rm in}={\it\Delta}U+W_{\rm out}=nC_p T\,\biggl (=\frac{5}{2}nR{\it\Delta}T=\frac{5}{2}P{\it\Delta}V\biggr)\\\\ &\gamma=\frac{C_p}{C_V}\,\biggl(=\frac{5}{3}\biggr)\end{align}\] |
定圧変化
| \[\begin{align}&上から,\;シャルルの法則,\;熱力学第一法則.&&\\\\ &P=Const.\quad\longrightarrow\quad\frac{V}{T}=Const.\\\\ &Q_{\rm in}={\it\Delta}U+W_{\rm out}=nC_p{\it\Delta}T\end{align}\] |
定積変化
| \[\begin{align}&上から,\;ボイル・シャルルの法則,\;熱力学第一法則.&&\\\\ &V=Const.\quad\longrightarrow\quad\frac{P}{T}=Const.\\\\ &W_{\rm out}=0\quad\longrightarrow\quad Q_{\rm in}={\it\Delta}U=nC_V {\it\Delta}T\end{align}\] |
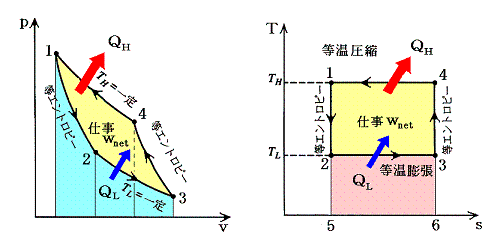
等温変化
| \[\begin{align}&上から,\;ボイルの法則,\;熱力学第一法則.\\\\ &T=Const.\quad\longrightarrow\quad PV=Const.\\\\ &{\it\Delta}U=0\quad\longrightarrow\quad Q_{\rm in}=W_{\rm out}=P{\it\Delta}V \end{align}\] |
断熱変化
| \[\begin{align}&上から,\;気体の状態方程式,\;熱力学第一法則,\;ポアソンの法則.&& && &&\\\\ &PV=nRT\\\\&Q_{\rm in}=0\quad\longrightarrow\quad {\it\Delta}U+W_{\rm out}=0\\\\ &PV^\gamma=Const.\quad\longrightarrow\quad TV^{\gamma-1}=Const.\end{align}\] |
マイヤーの法則
ポアソンの法則に関連して使う.
| \[\begin{align}&C_p-C_V=R\quad\longrightarrow\quad \frac{C_V}{R}=\frac{1}{\gamma-1},\quad \frac{V_p}{R}=\frac{\gamma}{\gamma-1}\\\end{align}\] |
熱効率
| \[e=\frac{W_{\rm out}}{Q_{\rm in}}=1-\frac{{\Delta}U}{Q_{\rm in}}\] |
波
基本事項
どの方向に注目すれば解けるのか,解きやすいのかを常に考える.
正射影ベクトルが有効か考える.
同心円状に広がる波の速度は,成分表示してみると良いことがある.
定在波の節と腹は時間を少し動かして調べる.
基礎方程式
波の速さを \(v\),振動数を \(f\),波長を \(\lambda\) として,
| \[v=f\lambda\] |
波動関数
| \[y=A\sin(\omega t-kx)=A\sin \tau\biggl(\frac{t}{T}-\frac{x}{\lambda}\biggr)\] |
波面
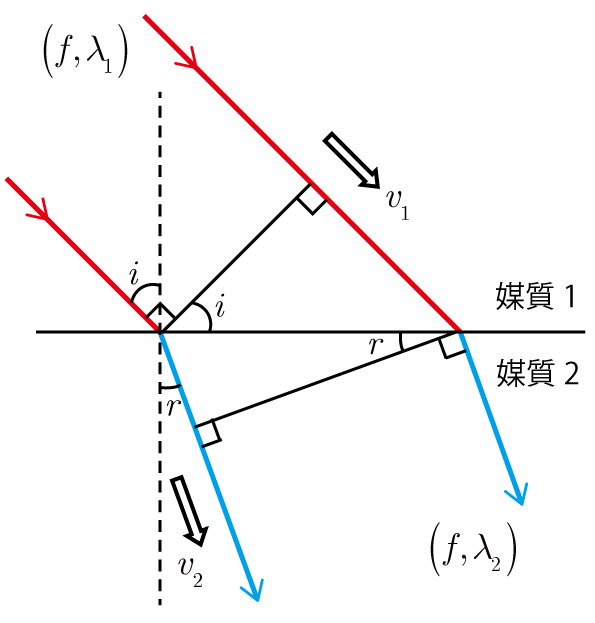
反射・屈折
基礎方程式
| \[\frac{1}{a}-\frac{1}{f}=\frac{1}{b}\] |
凸レンズ・凹レンズについて,媒質間の屈折率が逆になったら互いに逆の性質(凝集・拡散)を帯びる.
干渉
焦点の位置が求められる場合に使う.
同位相波源を点 \(\rm F_1,\,F_2\),波長を \(\lambda\) として,波を点 \(\rm P\) で観測するとき,
| \[{\rm PF_1-PF_2}=n\lambda\qquad\begin{cases} \text{nは整数}&\Leftrightarrow\text{Pは腹}\\ \text{nは半整数}&\Leftrightarrow\text{Pは節}\end{cases}\] |
焦点の位置が求めにくい場合,以下を使う.
点 \(\rm P\) での位相を \(\theta_1,\,\theta_2\) として,
| \[\theta_1-\theta_2=\tau n\qquad\begin{cases} \text{nは整数}&\Leftrightarrow\text{Pは腹}\\ \text{nは半整数}&\Leftrightarrow\text{Pは節}\\\end{cases}\] |
スリット実験
少しずつぼやけて三角関数的に
| スリットの本数 | 腹条件 |
|---|---|
| \(2\) | \(\dfrac{d}{l}x\equiv0\mod\lambda\) |
| \(\vdots\) | \(\vdots\) |
| \(2k\) | \(\dfrac{kd}{l}x\equiv0\mod\lambda\) |
| \(\vdots\) | \(\vdots\) |
| たくさん | \(d\sin\theta\equiv0\mod\lambda\) |
弦の性質
波の速さを \(v\),弦の張力を \(T\),弦の線密度を \(\rho\) として,
| \[v=\sqrt{\frac{T}{\rho}}\] |
両側固定端
| \[\frac{n}{2}\lambda=L\] |
片側開口端
波長を \(\lambda\),筒の長さを \(L\),開口端補正を \({\it\Delta}L\) として,\(
n\) 倍振動のとき,
| \[\biggl(\frac{1}{2}n-\frac{1}{4}\biggr)\lambda=L+{\it\Delta}L\] |