分野




総則
- 関数 \(f(x)\) と曲線 \(y=f(x)\) を区別する.
最大値・最小値
総則
等号成立するか常に確認する.
条件の検証
2点の \(x\) 座標の大小が常に成立するか調べる際,等号成立条件を検討し,成立しない場合は反例を1つ提示する.
解の限定
最初に条件から解の候補を絞る.
AM-GM不等式
最初に使えないか疑う.
| \[\begin{align}&正の定数\,a_i\,に対し,\\\\ &\frac{1}{n}\sum_{i=0}^{n-1} a_i\ge\sqrt[n]{\prod_{i=0}^{n-1} a_i}\quad(a_i\ge0)\\\\ &等号成立条件は,\,a_0=a_1=\cdots =a_{n-1}&&\end{align}\] |
コーシーシュワルツの不等式
2番目に使えないか疑う.
| \[\begin{align}&任意のベクトル\,\boldsymbol{A},\,\boldsymbol{B}\,に対し,\\\\ &\begin{aligned}&|\boldsymbol{A}|^2 |\boldsymbol{B}|^2 \ge(\boldsymbol{A}\cdot\boldsymbol{B})^2\\\\ \Leftrightarrow\quad&\biggl(\sum_{i=1}^n a_i^2\biggr) \biggl(\sum_{i=1}^n b_i^2\biggr) \ge\biggl(\sum_{i=1}^n a_i b_i\biggr)^2\quad(a_i,\,b_i\in\mathbb{R})\end{aligned}\\\\ &等号成立条件は,\boldsymbol{A}=k\boldsymbol{B}\quad (k\ne0)\end{align}\] |
線形計画法
求数が実質1次ときに使える.
微分よりも楽にできそうなら使う.
求数をまとめてから計算する.
円に対しては,点と直線の距離を忘れずに.
点 \((a,b)\) を中心とする曲線 \(y=f(x)\) の最小接円は,グラフ上の点を \((p,\,f(p))\) とおき,中心と三平方の定理を満たす \(p\) の最小値から求めることもできる.
その他有名不等式
| \[\begin{align}&[x]<x<[x]+1\\\\&1+x\le e^x\end{align}\] |
傾き
以下の形になっていないか調べる.
| \[\frac{y(t)-b}{x(t)-a}\] |
微分
最終手段.
特定の定義域・値域
- 境界条件の確認
- 極値の確認
分数・根号
| \[{\rm ex)}\quad\frac{1}{f(x)\sqrt{g(x)}}\quad\rightarrow\quad \bigl(f(x)\bigr)^2g(x)\;を調べる.\] |
変数の削減
| \[{\rm ex)}\quadf(x)+g(x)=Const.\quad\rightarrow\quadf(x)g(x)=f(x)\bigl(a-f(x)\bigr)\] |
ラグランジュの未定乗数法
確かめで使えるかも.
最大値・最小値を求めたい関数を \(f(\boldsymbol{x})\),制約を \(g(\boldsymbol{x})=0\) として,
| \[L(\boldsymbol{x},\lambda)=f(\boldsymbol{x})-\lambda g(\boldsymbol{x}),\quad \boldsymbol{\nabla}L=0\] |
不等式制約の場合,さらに \(\boldsymbol{\nabla}f(\boldsymbol{x})\) で解の候補を求め,制約を確認する.
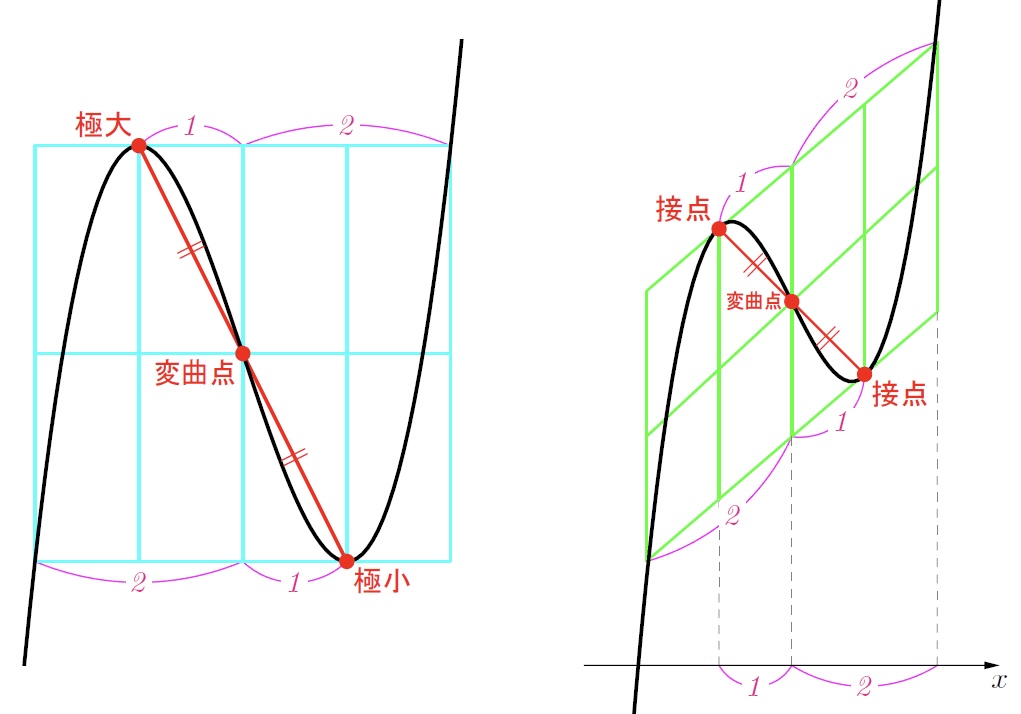
3次関数
8分割パレッドを使うと解きやすいことがある.
極限
関数の強さ
| \[\lim_{x\rightarrow\infty} \frac{\ln x}{x^n}=\frac{x^n}{e^x}=\frac{e^x}{x!}=0\qquad(n>0)\] |
有名極限
ネイピア数
| \[\lim_{x\rightarrow\infty} \biggl(1+\frac{1}{x}\biggr)^x =\lim_{n\rightarrow 0}\,(1+x)^{\frac{1}{x}}=e \quad\Leftrightarrow\quad\lim_{x\rightarrow 0} \frac{\ln(1+x)}{x}=1\] |
冪乗
| \[\lim_{x\rightarrow\infty} x^n=\begin{cases}\begin{aligned} &0&&(n<0)\\\\&1&&(n=0)\\\\&\infty&&(n>0)\end{aligned}\end{cases}\] |
有名挟撃
| \[\begin{align}&-1\le\sin\theta\le 1\qquad-1\le \cos\theta\le 1\\ &1-x<\sqrt{1-x^n}<1\qquad(0\le x\le 1\le n)\end{align}\] |
平均値の定理
\(f(b)-f(a)\) の形を,見つけたり,無理矢理作ったりして使う.
| \[\begin{align}&定数\,a’<a<b<b’,\quad f(x)\,が\,a’<x<b’\,で微分可能.\\\\ \Bigl(\Longrightarrow\quad&f(x)\,が\,a\le x\le b\,で連続かつ\,a<x<b\,で微分可能.\Bigr)\\\\ \Longrightarrow\quad&\frac{f(b)-f(a)}{b-a}=f’(c)\quad(a<c<b)\quad を満たす\,c\,が存在.&& \end{align}\] |
微分
連続
| \[f(x)\,が\,x=a\,で連続.\quad\Leftrightarrow\quad f(x)|_{x=a}=f(a)\quad\land\quad\lim_{x\rightarrow a}f(x)=f(a)\] |
微分可能性
| \[\begin{align}&f(x)\,が\,x=a\,で微分可能.\\\\\Leftrightarrow\quad&f(x)\,が\,x=a\,で連続. \quad\land\quad\lim_{h\rightarrow0}\frac{f(a+h)-f(a)}{h}=f’(a)&&\end{align}\] |
微分公式
| \[\begin{align}&\frac{d}{dx}x^n=\begin{cases}nx^{n-1}&(n\ne-1)\\\\ \log x &(n=-1)\end{cases}\\\\&\frac{d}{dx}e^x=e^x\\\\ &\frac{d^2}{dx^2}\sin x=\frac{d}{dx}\cos x=-\sin x\end{align}\] |
増減表
作図等で使う.
ex) \(x\ge 0\) で定義され,\(\alpha\) に収束する単調増加関数に対し,
| \(x\) | \(0\) | \(\cdots\) | \((\infty)\) |
| \(f’(x)\) | \(\bigl(f’(0)\bigr)\) | \(+\) | \((0)\) |
| \(f’’(x)\) | \(\bigl(f’’(0)\bigr)\) | \(-\) | |
| \(f(x)\) | \(f(0)\) | ↱ | \((\alpha)\) |
媒介変数表示
ex) \(0\le x\le \tau\) で定義されるある閉凸曲線に対し,
| \(t\) | \(0\) | \(\cdots\) | \(t_0\) | \(\cdots\) | \(t_1\) | \(\cdots\) | \(\tau\) |
| \(\dot{x}\) | \(+\) | \(0\) | \(-\) | \(-\) | |||
| \(x\) | \(0\) | → | \(x_0\) | ← | \(x_1\) | ← | \(0\) |
| \(\dot{y}\) | \(+\) | \(+\) | \(0\) | \(-\) | |||
| \(y\) | \(0\) | ↑ | \(y_0\) | ↑ | \(y_1\) | ↓ | \(0\) |
テイラー展開
| \[f(x)=\sum_{n=0}^\infty \frac{f^{(-n)}(a)}{n!}(x-a)^n\] |
接線
接点を設定してから求める.
\(y=f(x)\) の \(P\bigl(p,\,f(p)\bigr)\) での接線を \(\ell:\,y=\ell(x)\) として,
| \[\ell(x)=f(p)+f’(p)(x-p)\] |
凸グラフの外側から引ける接線は2本.
一次近似
| \[f(\alpha)\approx f(a)+f’(a)(\alpha-a)\quad\Leftrightarrow\quad [F(t)]_c^\alpha\approx[F(t)]_c^a+f(a)(\alpha-a)\] |
積分
総則
- 不定積分は,一番最初に\(+C\)を強調しておく.
- 定積分で分数が現れた場合,一度約分せずに展開する.
- 置換積分を行うときは,一度,結果をそのまま書く.
- 定積分は,同じ面積や打ち消す面積を考えて計算を減らす.
- 偶奇関数,周期関数,3次関数での変曲点対称など
原始関数
原始関数を知っているか調べる.
King Property
三角関数が多めの式や定積分で行き詰まったときに使う.
| \[\int_a^b f(x)dx=\int_a^b f(a+b-x)dx\] |
倍角の公式
三角関数の積分は,これで次数下げができないか調べる.
| \[\begin{align}&\cos2\theta=\cos^2\theta-\sin^2\theta &&\sin2\theta=2\cos\theta\sin\theta\\\\ &\cos3\theta=-3\cos\theta+4\cos^3\theta&&\sin3\theta=3\sin\theta-4\sin^3\theta\\\\ &1+\cos{\theta}=2\cos^2{\frac{\theta}{2}}&&1-\cos{\theta}=2\sin^2{\frac{\theta}{2}}\\\\ &\sqrt{1+\cos{\theta}}=\sqrt{2}\left|\cos{\frac{\theta}{2}}\right| &&\sqrt{1-\cos{\theta}}=\sqrt{2}\left|\sin{\frac{\theta}{2}}\right|\\\\ &1\pm\sin{\theta}=\biggl(\cos{\frac{\theta}{2}}\pm\sin{\frac{\theta}{2}}\biggr)^2 \end{align}\] |
微分形の接触
以上に当てはまらない場合,この形がないか調べる.
| \[\begin{align}&\int f\bigl(g(x)\bigr)\,g’(x)\;dx=F\bigl(g(x)\bigr)+C\\\\ &特に,f(x)=\frac{1}{x}\,のとき,\\\\&\int \frac{g’(x)}{g(x)}\;dx=\ln g(x)+C\end{align}\] |
部分積分
微分形の接触もない場合,これが有効か考える.
対数積分は,対数を微分側で用いる.
計算ミスが起こりやすいので,符号の取り扱いは丁寧に.
他には,指数関数や三角関数の積,\(\frac{1}{\cos^2\theta}\) など見つけたときや,式の形を変えたいときに使う.
| \[\int fg\,dx=fG-\int f’G\,dx\] |
使える場合は瞬間部分積分を使う.(()内の数字は,微分で下がり,積分で上がる)
| \[\int f^{(0)}g^{(0)}dx=f^{(0)}g^{(1)}-f^{(-1)}g^{(2)}+f^{(-2)}g^{(3)}-\cdots+C\] |
部分分数分解
部分積分が厳しそうな場合,分母の冪乗の式を因数分解できないか考える.
以下は主な部分分数分解.
| \[\frac{1}{1-M^2}=\frac{1}{2}\biggl(\frac{1}{1-M}+\frac{1}{1+M}\biggr)\] |
置換積分
以上が厳しそうな場合,置換積分を考える.
タンジェント置換
以下のように変形して積分漸化式.
| \[\int\frac{t^n}{1+t^2}\,dt=\int\tan^n\theta\,d\theta\] |
双曲線関数置換
変域がうまく合っているときに使う.
| \[\int\underset{\ge 1}{\underline{\cosh x}}\;dx=\sinh x+C\,,\quad \int\underset{\mathbb{R}}{\underline{\sinh x}}\;dx=\cosh x+C\] |
特に,三角関数を置換する場合,\({\rm arcsinh}\,x=\log(\sqrt{x^2+1}+x)\) より,
| \[\cos\theta=\frac{1}{\cosh\varphi}\,,\quad\sin\theta=\tanh \varphi\,,\quad \tan\theta=\sinh\varphi\\\\ \int_{\theta_0}^{\theta_1}\;d\theta\quad\rightarrow\quad \int_{\log\frac{1+\sin\theta_0}{\cos\theta_0}}^{\log\frac{1+\sin\theta_1}{\cos\theta_1}} \frac{1}{\cosh\varphi}\;d\varphi\] |
また,双曲線関数の関係は,
| \[\begin{align}&\cosh^2\varphi-\sinh^2\varphi=1 &&1-\tanh^2=\frac{1}{\cosh^2\varphi}=\bigl(\tanh x\bigr)’\\\\ &\cosh2\varphi=\cosh^2\varphi+\sinh^2\varphi &&\sinh2\varphi=2\cosh\varphi\sinh\varphi\end{align}\] |
ワイエルシュトラス置換
同周期の三角関数のみの式に対し,行き詰まったときに使う.
| \[\begin{align}\tan{\frac{\theta}{2}}=t\quad\cos{\theta}=\frac{1-t^2}{1+t^2}\quad \sin{\theta}=\frac{2t}{1+t^2}\quad\tan{\theta}=\frac{2t}{1-t^2}\end{align}\] |
その他の置換
三角関数の逆関数
三角関数の逆関数に正関数を作用させたときは,図形的解釈で値を求める.
定積分型微分方程式
非被積分部を外に出して新たな関数または定数として定義する.
積分漸化式
ウォリス積分
| \[\begin{align}&\begin{aligned}I_n&=\int_0^{\frac{\tau}{4}} \cos^nx\;dx \quad\biggl(=\int_0^{\frac{\tau}{4}} \sin^nx\;dx\biggr)\\\\ &=\int_0^{\frac{\tau}{4}} \cos^{n-1}x\,(\sin x)’\;dx\\\\ &=(n-1)\int_0^{\frac{\tau}{4}} \cos^{n-2}x\,(1-\cos^2 x) x\;dx\\\\ &=(n-1)I_{n}-(n-1)I_{n}\\\\\end{aligned}\\\\ \Leftrightarrow\quad&I_{n}=\frac{n-1}{n}I_{n-2}\\\\\Leftrightarrow\quad &I_{n}=\begin{cases}\frac{(n-1)!!}{n!!}&(n\equiv1\mod2)\\\\ \frac{\tau}{4}\frac{(n-1)!!}{n!!}&(n\equiv0\mod2)\end{cases}\end{align}\] |
\(\tan^n x\)
| \[\begin{align}I_n&=\int_0^{\frac{\tau}{8}} \tan^nx\;dx\\\\ &=\int_0^{\frac{\tau}{8}} \tan^{n-2}\biggl(\frac{1}{\cos^2x}-1\biggr)\;dx\\\\ &=\int_0^{\frac{\tau}{8}} \tan^{n-2}(\tan x)’\;dx-\int_0^{\frac{\tau}{8}} \tan^{n-2}x\;dx\\\\ &=\frac{1}{n-1}-I_{n-2}\\\\\end{align}\] |
\(\frac{1}{\cos^n x}\)
| \[\begin{align}&&&\begin{aligned}I_n&=\int \frac{1}{\cos^n x}\,dx\\\\ &=\int\frac{(\tan x)’}{\cos^{n-2}}\,dx\\\\ &=\frac{\tan x}{\cos^{n-2} x}-\int\frac{-(n-2)}{\cos^{n-1} x}(-\sin x)\tan x\,dx\\\\ &=\frac{\tan x}{\cos^{n-2} x}-(n-2)\int\frac{1-\cos^2 x}{\cos^{n} x}\,dx\\\\ &=\frac{\tan x}{\cos^{n-2}}-(n-2)(I_n-I_{n-2})\end{aligned}\\\\ &\Leftrightarrow&&I_n=\frac{1}{n-1}\frac{\tan x}{\cos^{n-2}}+\frac{n-2}{n-1}I_{n-2} \end{align}\] |
ベータ関数
| \[\int_a^b (x-a)^m (b-x)^n dx=\frac{m!n!}{(m+n+1)!}(b-a)^{m+n+1}\] |
特に,共テなどで以下の形で計算する場合などは符号に注意.
| \[\int_\alpha^\beta(x-\alpha)(x-\beta)\,dx=-\frac{1}{6}(\beta-\alpha)^3\] |
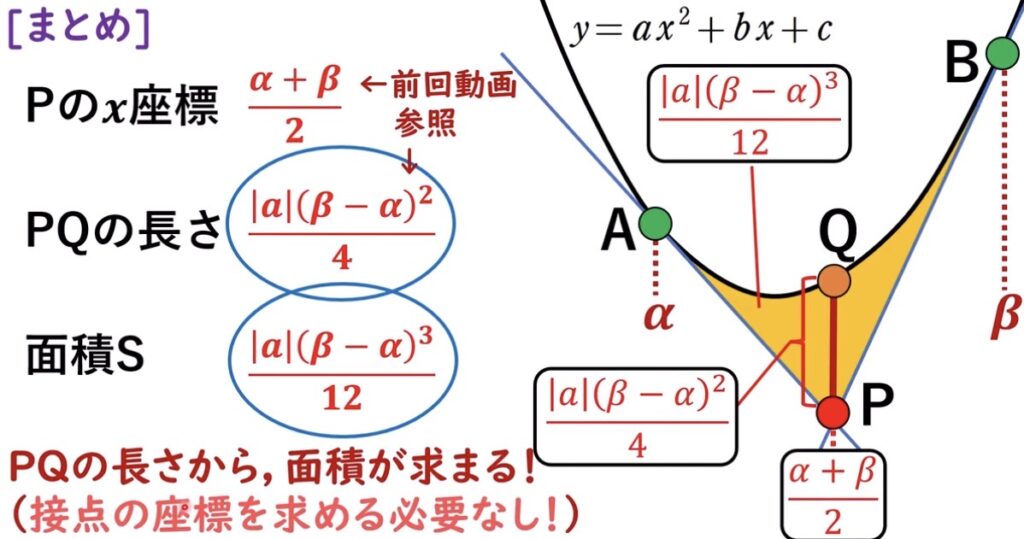
2次関数の性質と\(\frac{1}{12}\)公式
2次関数C上の2点A,Bの\(x\)座標\(\alpha,\beta\)に対し,A,Bそれぞれでの接線の交点の\(x\)座標は\(\frac{\alpha+\beta}{2}\)であり,その3線で囲まれた面積は,C\(,\alpha,\beta\)にベータ関数を適用した値の半分.
シンプソンの公式
\(f(x\)) が3次以下の冪級数の場合,厳密に等式となる.
3次以下の冪級数の定積分速くを求めるときに使う.
| \[\int_\alpha^\beta f(x)\approx \frac{1}{6}\Biggl(f(\alpha)+4f\biggl(\frac{\alpha+\beta}{2}\biggr)+f(\beta)\Biggr)\] |
計量
回転積分
積分範囲に被りがある場合,それを除いてから積分する.
| \[V=\int_a^b \frac{1}{2}\tau\, \bigl(f(x)\bigr)^2\;dx\] |
バウムクーヘン積分
| \[V=\int_a^b \tau x\, |f(x)|\;dx\] |
傘型分割
\(y=mx\) を回転軸として,
| \[m=\tan\theta,\quad V=\int_a^b \frac{1}{2}\tau\,\bigl(mx-f(x)\bigr)^2\cos\theta\; dx \end{align}\] |
パップス=ギュルダンの定理
重心と回転軸との距離を \(\ell\),断面積を \(S\) として,
| \[V=\tau\ell S\] |
級数 × 積分
区分求積法
無限積に対しては,対数を取ってから区分求積法を適用する.
その際,最初に \(e\) の肩に乗せることを強調しておく.
級数の積分挟撃
級数の項の一部を外に出す場合がある.